Short dive into Conditional Probability - refresher 06 May 2015
I hope this to be one of the many to come short and to the point posts about different aspects of data analysis and how to tackle data analysing problems. The purpose of this is to be a short refresher course in different core aspects of machine learning and data analysis. This being said the first problem I tackle is the Conditional probability.
The mathematical definition of probability is a function on a subsets of a sample space which satisfy certain axioms. That doesn’t tell me much and it doesn’t make me think about anything in particular. More intuitively we can consider probabilities proportions. Saying that an event has the chance or the probability of one-sixth it means that the event occurs one-sixth of the time. This is a more intuitively interpretation and it suits our purpose.
Often we calculate a probability by dividing the number of favourable events (number of events when things go our way) to the total number of events. For example, we have a fair dice and we want to know what’s the probability of rolling an even number. Each of the six sides of the dice has an equal probability of 1/6 to occur after a roll, so the probability to roll an even number is equal to 3/6 = 1/2. Why this works is because each of the possibilities is equally likely by assumption (remember the fair dice).

Now that we’ve established what simple probability means, we want to know how often A occurs when we know that B has already occurred. This is basically what a conditional probability is. If we know that B occurred, then the occurrences of A are all and exactly those situations in which both A and B occur, and since we are assuming B occurred, then the total number of possibilities are reduced to only those were that happened.
| P(A | B) = #of occurrences of A and B / #of occurrences of B = P(A ∩ B) / P (B) |
This is best explained with an example and a Venn diagram.
We want to find the probability of rolling a dice and it’s value is greater than 3 and knowing that the value is an even number. We can write this as:
| P(A | B) = What is the probability of (Rolling a dice and its value is greater than 3 | knowing the value is an even number) |
We are going to roll a fair 6 sided dice. Event A = Rolling a dice and its value is greater than 3, so P(A) = 3/6 = 1/2 .
Event B = Rolling a dice and its value is an even number, so P(B) = 3/6 = 1/2 .
To get the probability of event A and event B happening, we can use the following Venn diagram.
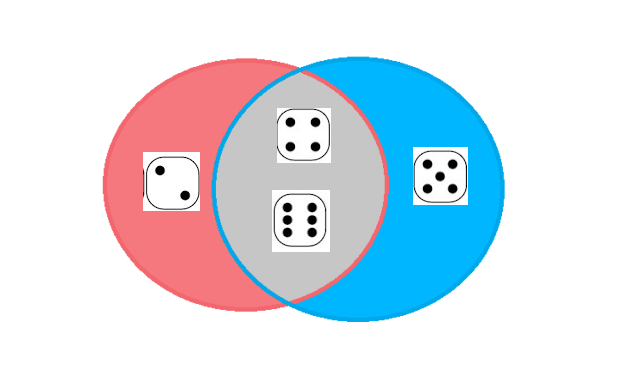
so P(A ∩ B) = 2/6 = 1/3
So what is the probability of event A happening if we know event B already happened:
| P(A | B) = P(A ∩ B) / P (B) = 1/3 * 2/1 = 2/3 |