Privacy in Location Based Services - Part 2 | ~elf11.github.io

Privacy in Location Based Services - Part 2 15 Jul 2017

In a previous post we discussed about Location Based Services (LBS), what they are, why are they important and what initial ways were there to achieve privacy in LBS and how that privacy was broken. In this post we are going to continue discussing about LBS and more specifically we are going to look at a few algorithms that were used back in the day for achieving it (back in the day means before they were proven to be total useless gatbage :p - just kidding, or am I?). Anyway, we are going to discuss two different types of algorithms for this. One of them requires a third party trusted architecture the other one doesn’t.

What is third party trusted architecture?

As we can see in the diagram below a trusted third party receives the exact locations from clients, blurs the locations, and sends the blurred locations to the server. The advantages of trusted third party architecture are that it provides powerful privacy guarantees with high-quality services. On the other hand there are problem with system bottleneck and sophisticated implementations.

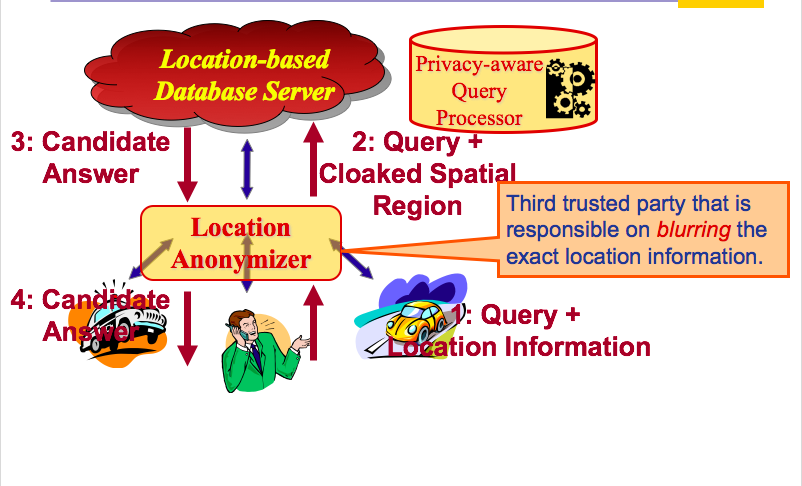
Hilbert k-anonymizing

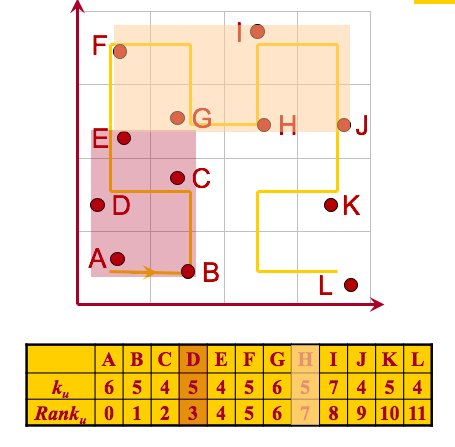
Hilbert k-anonymizing is a good example of the third party trusted architecture. How does it work? All user locations are sorted based on their Hilbert order. A Hilbert curve (also known as a Hilbert space-filling curve) is a continuous fractal space-filling curve that gives a mapping between 1D and 2D space that fairly well preserves locality. This means that if (x,y) are the coordinates of a point within the unit square, and d is the distance along the curve when it reaches that point, then points that have nearby d values will also have nearby (x,y) values. The converse can’t always be true. There will sometimes be points where the (x,y) coordinates are close but their d values are far apart.

To use the Hilbert curve for spatial cloaking and anonymization we we compute start and end values for an user u as:

start = rank(u) - (rank(u) mod k(u))
end = start + k(u) – 1

A cloaked spatial region is an Maximum Bounding Rectangle (MBR) of all users within the range (from start to end). The main idea is that it is always the case that k(u) users would have the sane [start,end] interval. A working example can be seen in the image below. Finding approximate nearest-neighbors using Hilbert order by sorting the objects based on their Hilbert values H(Oi). For a k-NN query q, the answer is the k objects with the smallest Hilbert distance to H(q). An offline anonymizer transforms all objects of interest using the Hilbert Order. The space transformation function is hidden from the server and the answer is approximate as it makes use of the locality preserving mapping of the Hilbert curve.

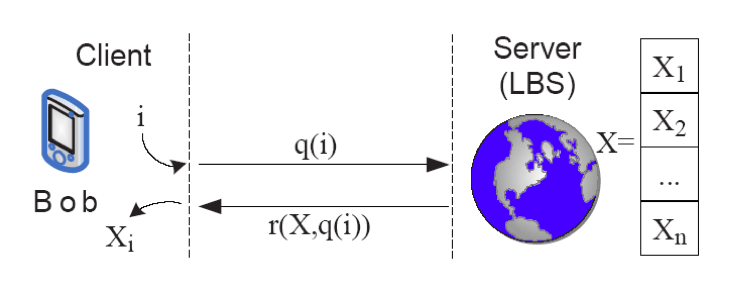
Private Information Retrieval (PIR)

PIR is a two-party cryptographic protocol where no trusted anonymizer is required and no trusted users are required. Other advantages of PIR: no pooling of a large user population required and no need for location updates, location data is completely obscured.

The way the framework works is illustrated in the image below. The framework doesn’t need an anonymizer, a client can privately retrieve information from a database, without the database server learning what particular information the client has requested. We can express the technique in a teorethical setting, where the database is an n-bit binary string X. The client wants to find the value of the i-th bit of X (X_i). To preserve privacy, the client sends an encrypted request q(i) to the server. The server responds with a value r(X, q(i)), which allows the client to compute X_i. Computational PIR that is discussed here employs cryptographic techniques, and relies on the fact that it is computationally intractable for an attacker to find the value of i, given q(i). Furthermore, the client can easily determine the value of X_i based on the server’s response r(X, q(i)).

This method has theoretical foundations, and we explain them below:

we have N a product of two very large prime numbers, N = q1*q2, where q1 and q2 large primes and we have the following two properties

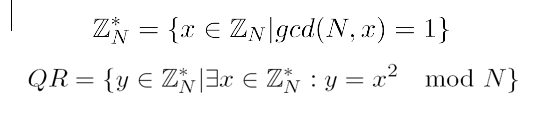
So we have the quadratic residuacity problem, which in computational number theory is a problem where given integers a and N, whether a is a quadratic residue modulo N or not. That’s what the two properties above say. But to decide if a number is QR/QNR is computationally hard. There are two properties of the Quadratic Residue (QR) and Quadratic Non-Residue that can help us in our computation though:

QR * QR = QR
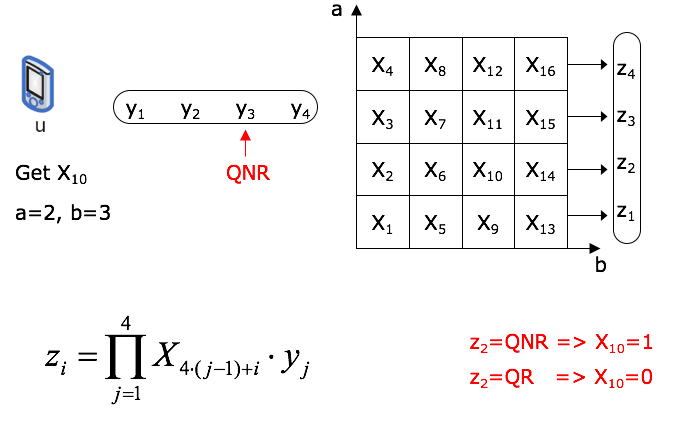
QR * QNR = QNR

This might all seem very confusing but below is a working example of the PIR protocol for binary data and n=16. u requests X10, which corresponds to M2,3. Therefore, u generates a message y = [y1, y2, y3, y4], where y1, y2, y4 are QR and y3 isn’t QNR. The server replies with the message z = [z1, z2, z3, z4]. If z2 ∈ QR then u concludes that X10 = 0, else X10 = 1.

Conclusion

Those were some techniques that have been used for location-data privacy. Most of them are outdated nowadays, differential privacy being the defacto standard (more on that in a future post), but they are still interesting from a scholarly point of view.