Fitting distributions to data in Python 29 Oct 2017

Those days I have been looking into fitting a Laplacian distribution to some data that I was having. The data was presented as a histogram and I wanted to know how the Laplacian distribution was looking over it. After some looking around and not too many straight ways to do it, I figured it out. The code is below and you should get something similar to what can be seen in the picture.

from scipy import stats  
import numpy as np  
import matplotlib.pylab as plt

# create some normal random noisy data
ser = 50*np.random.rand() * np.random.normal(10, 10, 100) + 20

# plot normed histogram
plt.hist(ser, normed=True)

# find minimum and maximum of xticks, so we know
# where we should compute theoretical distribution
xt = plt.xticks()[0]  
xmin, xmax = min(xt), max(xt)  
lnspc = np.linspace(xmin, xmax, len(ser))

# lets try the normal distribution first
m, s = stats.norm.fit(ser) # get mean and standard deviation  
pdf_g = stats.norm.pdf(lnspc, m, s) # now get theoretical values in our interval  
plt.plot(lnspc, pdf_g, label="Norm") # plot it

# exactly same as above
ag,bg = stats.laplace.fit(ser)  
pdf_laplace = stats.laplace.pdf(lnspc, ag, bg)  
plt.plot(lnspc, pdf_laplace, label="Laplace")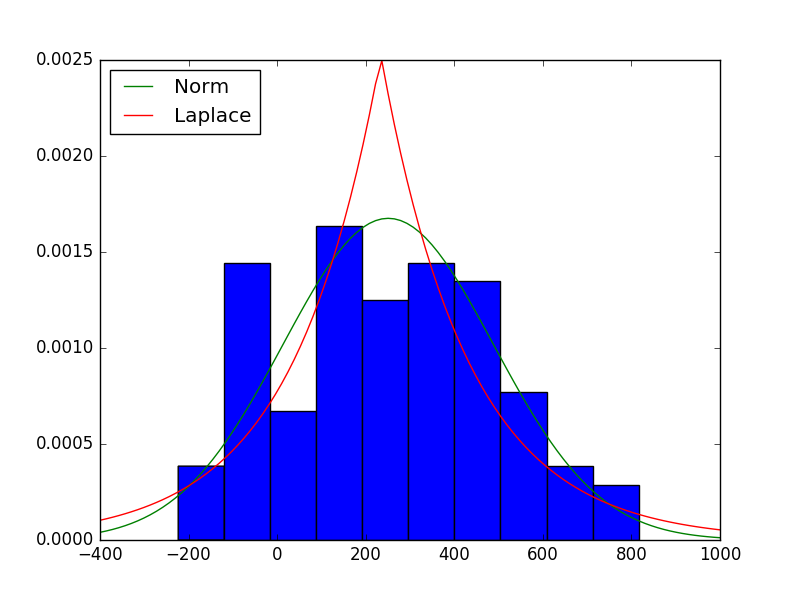
Fitting distributions to data

Happy Coding!